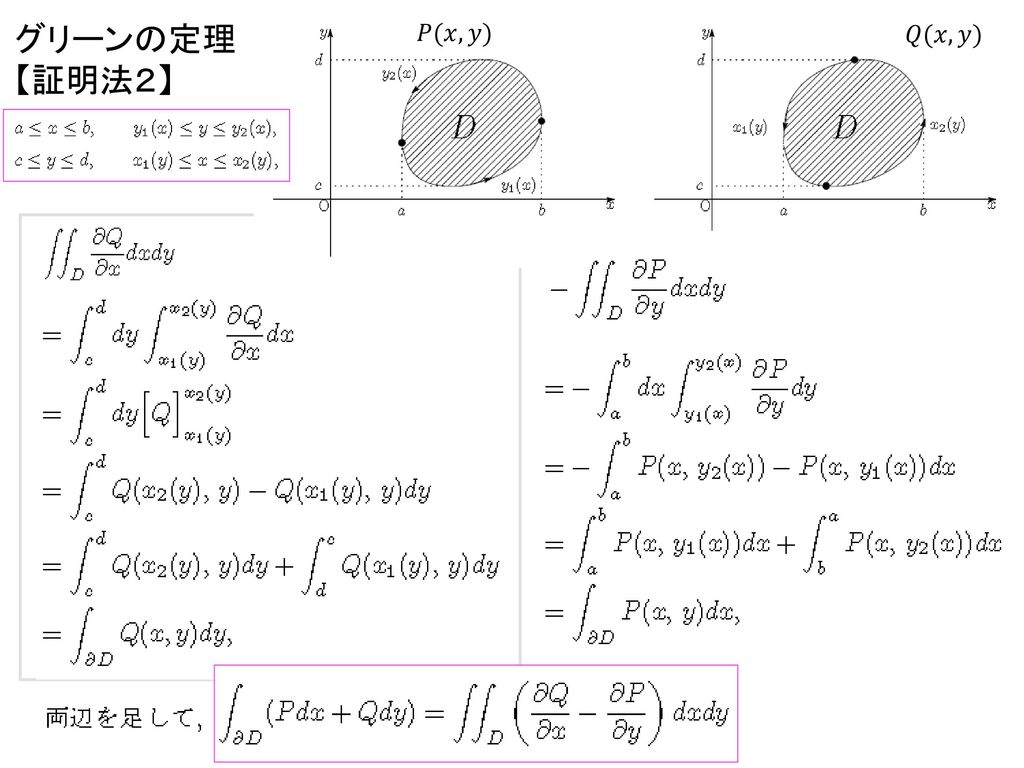
ガウス生誕の地(Brunswick)に建つガウスの像 面積分⇔体積分 ガウスの定理 ガウスの定理の(直感的)導出 P Q R 体積 の微小直方体を考える。 この微小直方体の表面 上での面積分: を計算する。 図21 積分面(ガウス面) ここで、n は積分面の単位法線グリーンの定理 単純閉曲線C(= @D) に囲まれた領域D について ∫ @D Pdx Qdy = ∫∫ D (@Q @x @P @y) dxdy 解説(高校数学との比較) 積分が1次元高い Version Pdx Qdy ! グリーンの第二定理から,もう一つ有用な定理が導かれます.式中,領域 は閉曲面 を境界とするものとし, は領域 で定義される,少なくとも 級の連続なスカラー関数とします. は 内の任意の点とし,点 における の値を と表記します.このとき,次の

グリーンの定理の証明と式の意味と例題 数学 複素関数論 ベクトル解析 Green S Theorem Youtube
ガウスグリーンの定理の証明
ガウスグリーンの定理の証明- まずは グリーンの定理 からはじめ、次回から ガウスの発散定理 と ストークスの定理 を示していきます。 線積分や面積分、体積積分を書き換えることができるこれらの定理は、電磁気学をはじめ様々な分野で活用することになりますので、証明の流れや ガウスグリーンの定理 x^2 3y^2 = 2 この楕円について y=x とで囲まれる部分のうち 右上の部分の面積を求める際に ガウスグリーンの定理を用いようとしたのですができませんでした どこがまちがっているのでしょうか? x=√2*cost y= (√6/3)*sint 積分区間はΠ/3



Mm Civil Tohoku Ac Jp
「有限要素法を学ぶときに出てきました。自分に対して分かりやすく書いたものは、恐らく他人にもわかりやすくなるだろうと思ってます。 学部時代にテストで出たのにさっぱり忘れた内容でした!」, キーワード 有限要素法,変分法,計算力学,数値解析,グリーンの定理,ガウスグリーンの 第28回 グリーンの定理 今回も最初は、ガウスの発散定理。 ガウスの発散定理 閉曲面 S で囲まれた領域 V において、ベクトル関数 A(x,y,z) の偏導関数が連続であれば、 そして、今回のテーマであるグリーンの定理を、このガウスの発散定理を使って証明するにゃ。これをグリーンの定理といいます。線積分と2重積分を変換する定理です。 とこんなことである。それで私には何だかよくわからないまま通過してしまったものである。 私の頭には、 ・ 何故変換定理が必
よく間違える例) 13P;QはDの境界、内部ともにC1級である。そうでない場合、グ リーンの定理は成り立たない Cを単位円に反時計回りに向き付けしたものとする I= ∫ C y x2 y2 dx x x2 y2 dy を求める。 @ @y (y x2 y2 @x (x x2 y2 x2 y2 (x2 y2)2なので、形式的にグリーンの定理を用いるとI=ガウス・グリーンの定理 エッセイ・評論 xy平面上において、tについての関数x (t),y (t)は微分可能でその導関数は連続であるとする。 t=αからt=βまで、tの増加とともにP (x (t),y (t))は原点Oの回りを左回りに回る。 このとき、t=αからt=βまでIntro02 2 • 偏微分方程式の数値解法(重み付き残差法) • ガウス・グリーンの定理 • 偏微分方程式 の 数値解法 ( 変分法 )
FEMintro 2 • 有限要素法入門 • 偏微分方程式の数値解法(重み付き残差法) • ガウス・グリーンの定理 • 偏微分方程式の数値解法(変分法)これをグリーンの第一公式という. また, ( )= 2 ( )= 2 両式を引き算して, ( – )= 2 – 2 これにガウスの定理を適用すると (φ∇ψ – ψ∇φ ) ⋅ dS S = φ∇2ψ – ψ∇2φ dv V これをグリーンの第二公式というさらに,グリーンの定理より = ∫∫ D (p G)uududv 一方曲面S のガウス曲率K(u,v) は K(u,v) = ¡ (p G)uu p G であるから(曲面の第1基本形式と第2基本形式の関係の7ページ) = ¡ ∫∫ D K(u,v) p Gdudv したがって, p ∫ Gdudv は面積要素でdσ とおけば C kgds = ∫ C dθ ¡ ∫∫ D K



講師 幹 浩文 A314 Ta 西方良太 m1 A305 Ppt Download



ストークスの定理 Tsujimotterのノートブック
グリーンの定理 の用例・例文集 上式は、主定理の右辺を、グリーンの定理に帰着する過程に他ならない。この式はグリーンの定理の特別な場合とみなすことが出来る。この定理を証明する簡単な方法として、1 つにはグリーンの定理を の勾配に適用する方法がある。グリーンの公式 例題 C をy = x とy = x2 (0 ≤ x ≤ 1) からなる閉曲線とし I = Z C (xy x2)dxx2dy とする。 1 線積分I を計算せよ。 2 グリーンの公式を用いて重積分に直してI を計算せよ。 解答例 とす212 グリーンの定理 • K氏:次に、グリーンの定理だが、これはガウスの定理の表面積分と体積積分の関係を変形した ものなんだ。閉曲面S で囲まれた領域V において、2つの異なるスカラ関数u、v に対し Z V (u∇2v ∇u·∇v)dV =Z S u ∂v ∂n dS = Z S un·∇vdS (12) Z V (u∇2v −v∇2u)dV =



媒介変数表示されたグラフの面積の求め方を例題付きで解説 検算に使える定理も教えます 東大医学部生の相談室



ガウスグリーンの定理の入試への応用 高校数学の美しい物語
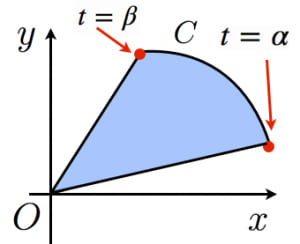
ガウス-グリーンの定理はパラメーター表示された曲線の面積を求めるときに 使用すると簡単に求まることがある。 例題1 半径 中心角 の扇形の面積Sを求めよ。 P (解)4 ガウス・グリーンの公式 定理44 Dを有限個のなめらかな曲線で囲まれる有界な閉集合とする. 境界を∂Dと書く.f,gがDでC1級の関数ならば ∫ ∂D f(x,y)dxg(x,y)dy= ∫ D (∂g ∂x ∂f ∂y) dxdy が成り立つ.ただし,∂Dの向きは進行方向左側にDの内部を見るよう に進むものとする.ちなみに従来の平面におけるグリーンの定理は,(1)式及び(2)式においてdz=0を代入すれば得られます。 関連記事 「3次元のグリーンの定理」の一般式 () 3次元空間におけるグリーンの定理(平面拡張版) () テーマ 数学



平面のグリーンの定理 物理のかぎしっぽ



3 13 ガウスの定理
(@Q @x @P @y) dx ^dy 微分 正式名称は 外微分 d(Pdx Qdy) @D D 境界ガウスの定理とグリーンの公式が同値であることは良く知られている 実際, グリーンの公式からガウスの定理を導くには で とおくと(だから) 同様に , および とおき, 得られた3式を辺々加えればガウスの定理が得られる 逆にグリーンの定理ガウスの定理 超関数の世界 第 章 解析学の舞台・・・関数の近似関数空間 関数を近似する フーリエ級数展開 複素数とオイラーの公式コーシーの定理 フーリエ変換 ソボレフ空間 関数の近似の道具軟化子 第




グリーンの定理の証明と式の意味と例題 数学 複素関数論 ベクトル解析 Green S Theorem Youtube




書記が数学やるだけ 30 線積分とグリーンの定理で面積を求める Malinka書記 Note
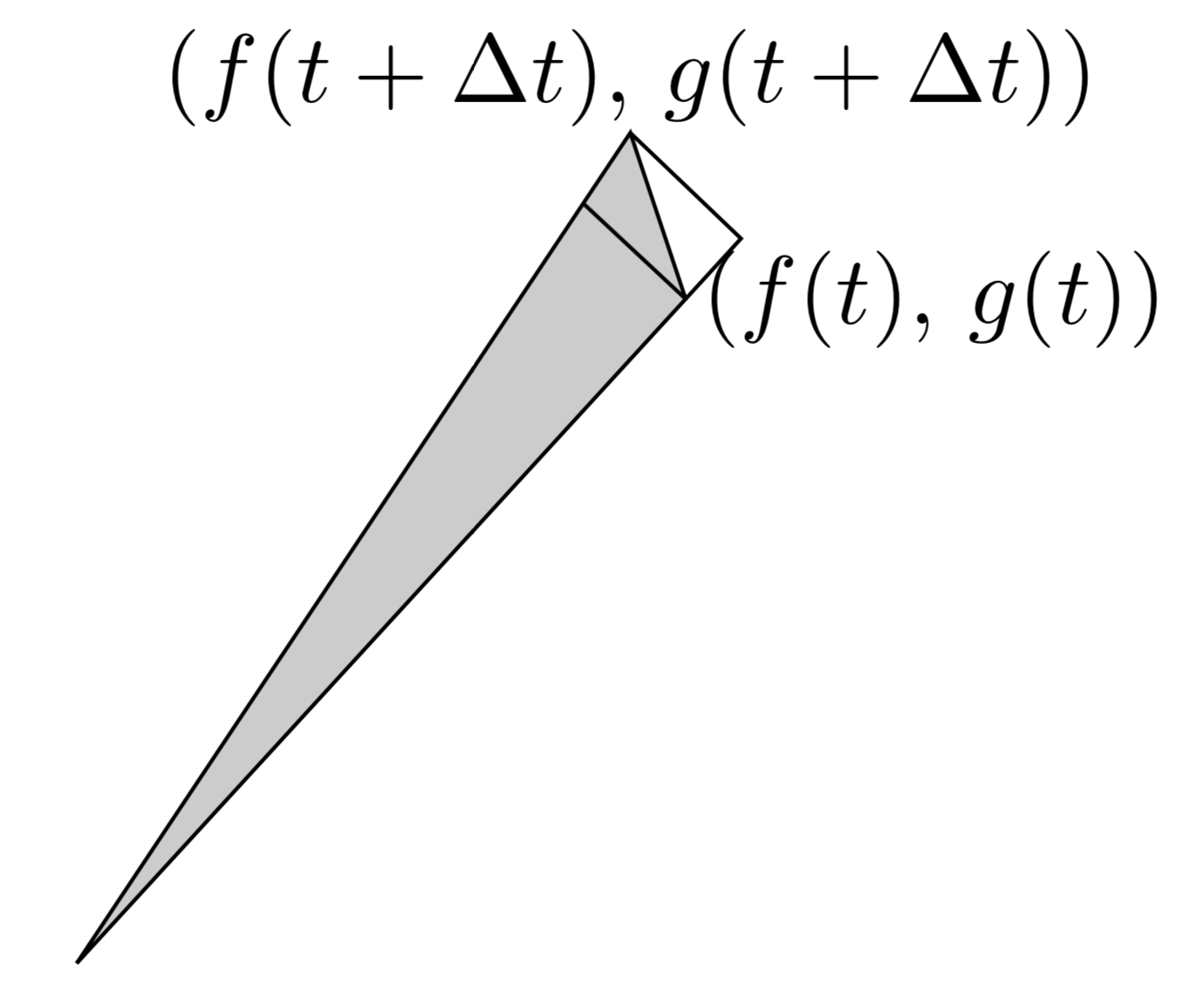
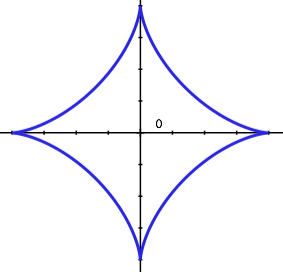
積分定理-gsg- 第1 話:グリーンの定理,第2 話:ストークスの定理,第3 話:ガウスの定理の積分3 定理についてのお話で す。いずれの定理も電磁気学や流体力学をはじめとして物理のいろんな分野で登場しますので慣れ親しんでおい て損はないと思います。GaussGreenの定理の証明 Step 1 符号つき面積 Oを原点とする座標平面上の OABに対し、原点から見てO(0, 0), A(a, b), B(c, d)が「左回りのとき正、右回りのとき負」・・・(*)となるような OABの面積を「符号つき面積」とよぶ。ガウスグリーンの定理を用いた楕円の面積公式の導出 発展的な内容です。楕円は x = a cos t, y = b sin t x=a\cos t,\y=b\sin t x = a cos t, y = b sin t と媒介変数表示されることを使います。媒介変数表示された曲線の面積を求める際は,ガウスグリーンの定理が




ガウスの発散定理 微小要素のイメージから分かりやすく証明 スモビュ




ガウス グリーンの定理 高校生ver Youtube
ガウス・グリーンの定理(平面におけるグリーンの定理) 左辺はS 上,右辺はC上のスカラーP, Q(ベクトルA⃗のx,y成分をP,Qと すると,∫2 次元のストークスの定理に等しい。) S (∂Q ∂x − ∂P ∂y) dxdy= I C (Pdx Qdy) (29) 13 1 1変数関数の部分積分 グリーンの定理は,1変数の関数の部分積分の公式に似ている.部分積分は,関数の積の微分 ( 19) から導ける.両辺を積分し,順番を入れ替えると ( ) となり,部分積分の公式が導かれた. このように単純な方法で導かれる部分グリーンの定理の別証 {1{ 定理 Dをxy平面の有界な領域で,その境界Cは互いに交わら ない有限個の区分的にC1 級の単一閉曲線からなっているとする そのときDを含む開集合でC1 級の関数f(x;y);g(x;y)に対して ∫∫ D (@g @x @f @y) dxdy= ∫ C fdxgdy が成り立つ ここで, CにはDに対して正の向きをつけて
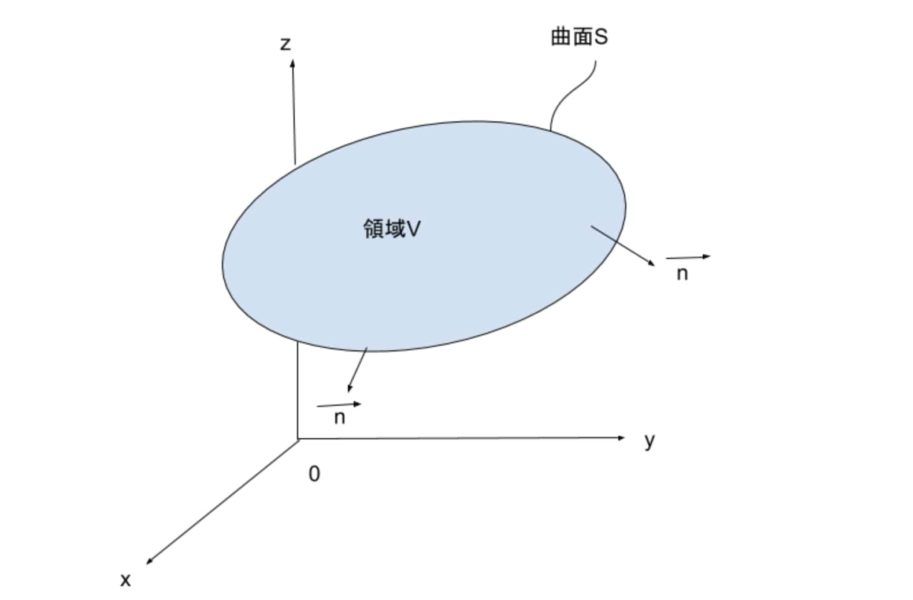



ガウスの定理の意味から証明まで 詳しく ベクトル解析 みやちゃのブログ



東大数学専科東大理系数学04年第3問
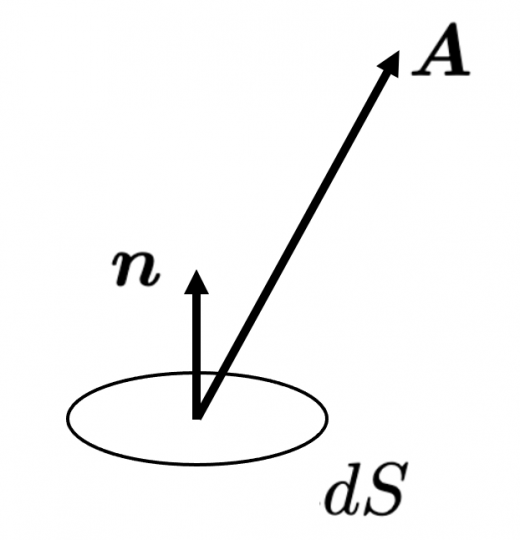



ガウスの発散定理 ストークスの定理の証明 高校数学の美しい物語



円錐面z 2 X 2 Y 2と平面z 1で囲まれる閉曲面をsとする ベクトル場 Yahoo 知恵袋



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配



1



Mm Civil Tohoku Ac Jp
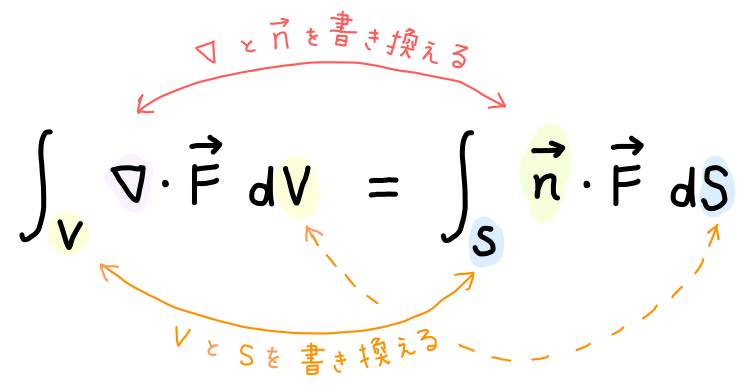



ガウスの発散定理 ベクトル解析 基礎からの数学入門
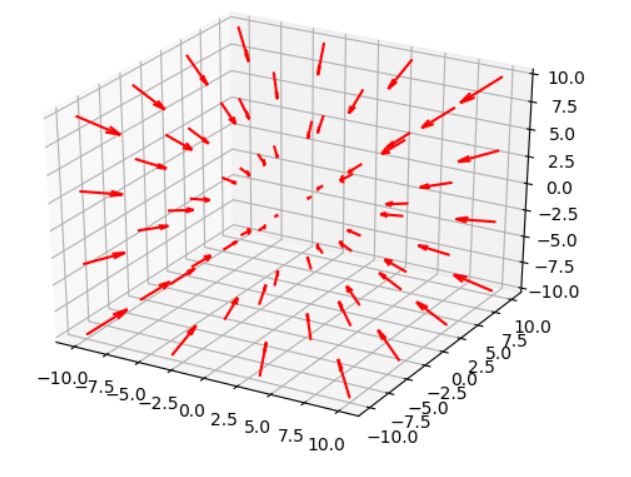



ガウスの発散定理とは 計算例 証明 電磁気学への応用 趣味の大学数学
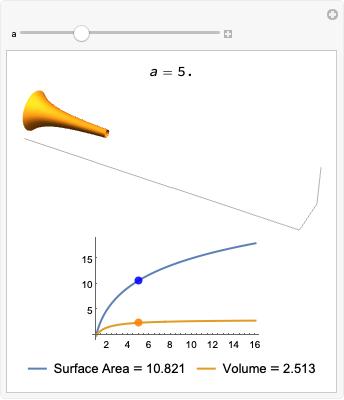



Integrate Wolfram言語ドキュメント
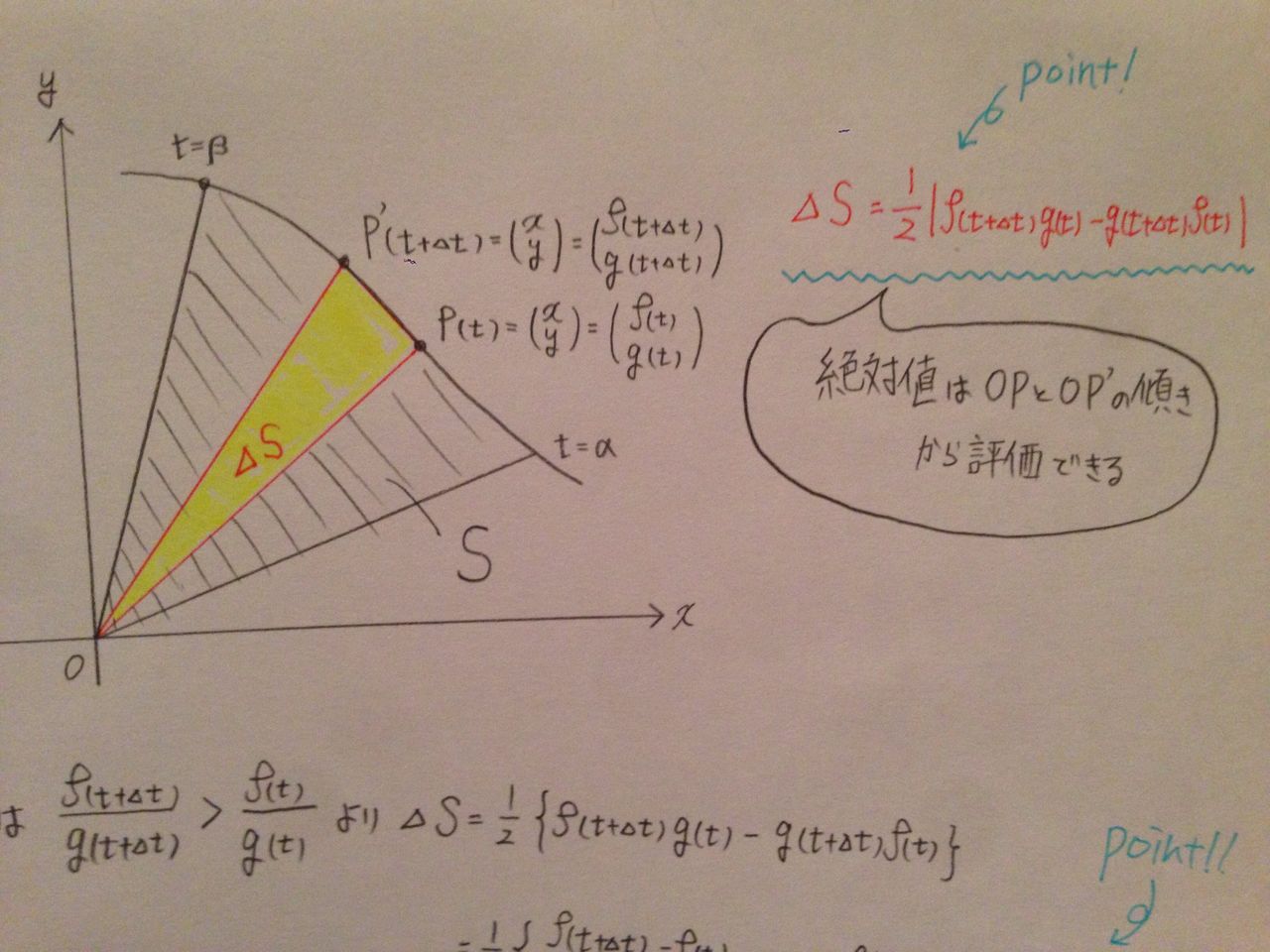



テラスハウス ガウス グリーンの定理 理系 落ちこぼれkの東大受験日記




数値解析 積分定理の応用 大学生 専門学校生 社会人 数学のノート Clearnote
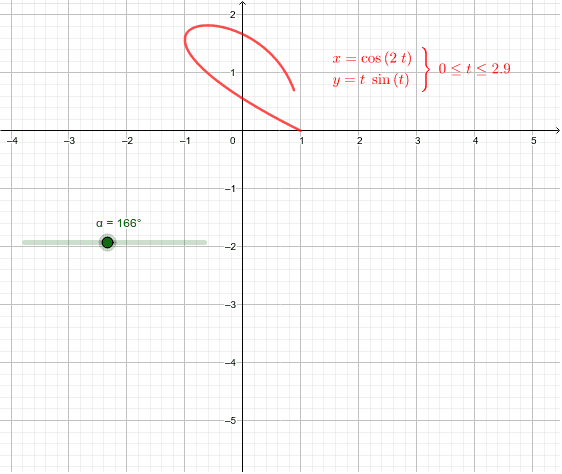



ガウスグリーンの定理の応用 Geogebra



ガウス の 定理




講師 幹 浩文 A314 微分 ベクトル解析 14 講師 幹 浩文 A314 A103 10 50 12 金 Ppt Download



グリーンの定理 積分定理の王



平面のグリーンの定理 物理のかぎしっぽ




講師 幹 浩文 A314 Ta 西方良太 m1 A305 Ppt Download
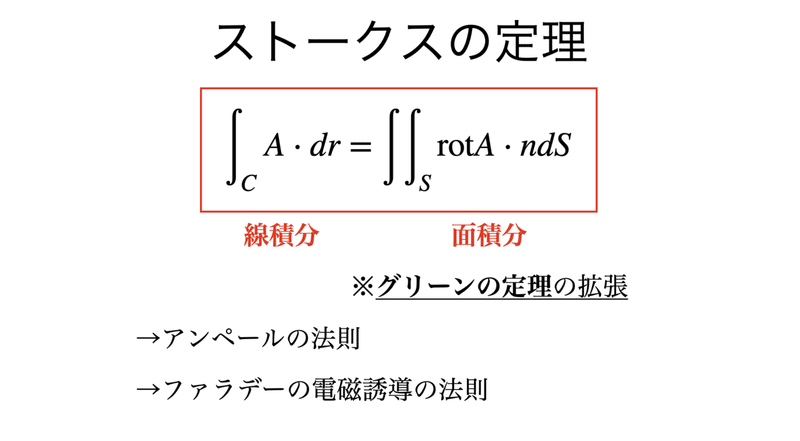



書記が数学やるだけ 135 ストークスの定理 ガウスの発散定理 連続の式 ヘルムホルツ分解 Malinka書記 Note



ストークスの定理再々考 物理のかぎしっぽ



ガウスの発散定理の問題です V X 2 Y 2 4 0 Z 3 ベ Yahoo 知恵袋



Math0 Pm Tokushima U Ac Jp




ガウスグリーンの定理をわかりやすく解説 大学生 専門学校生 社会人 Clearnote



ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門



ベクトル解析 わかりやすい 発散 Div のイメージ ガウスの発散定理 の証明 ばたぱら




ガウスグリーンの定理の入試への応用 高校数学の美しい物語




書記が数学やるだけ 135 ストークスの定理 ガウスの発散定理 連続の式 ヘルムホルツ分解 Malinka書記 Note



グリーンの定理 積分定理の王




ガウスグリーンの定理の応用 Geogebra



Math0 Pm Tokushima U Ac Jp




書記が数学やるだけ 135 ストークスの定理 ガウスの発散定理 連続の式 ヘルムホルツ分解 Malinka書記 Note




グリーンの定理からコーシーの積分定理へ 身勝手な主張



グリーンの定理 積分定理の王



グリーン ガウスの定理 流体力学



ガウスグリーンの定理の入試への応用 高校数学の美しい物語



グリーンの定理 積分定理の王




第13回 グリーン ガウス ストークスの定理
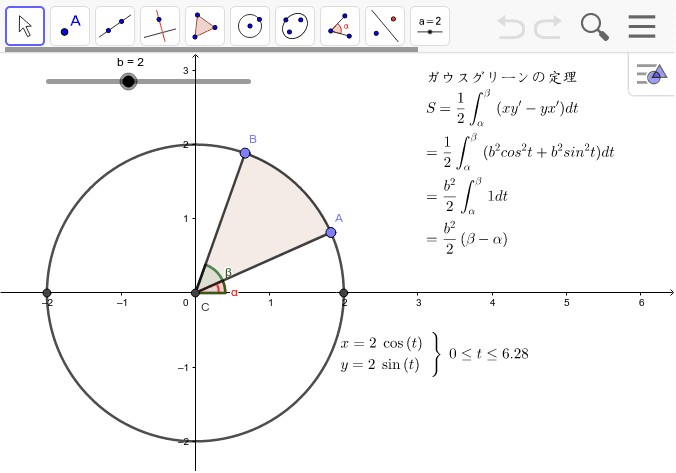



ガウスグリーンの定理 Geogebra



ときわ台学 ベクトル解析 グリーンの定理




ガウスグリーンの定理の応用 Geogebra



ガウスの発散定理



Ibe Kagoshima U Ac Jp




講師 幹 浩文 A314 微分 ベクトル解析 14 講師 幹 浩文 A314 A103 10 50 12 金 Ppt Download



グリーンの定理 積分定理の王




ガウスの発散定理 ストークスの定理の証明 高校数学の美しい物語



微分形式 多様体と電磁気学



3




アディショナルタイム説濃厚



グリーンの定理 積分定理の王




ガウス グリーン の 定理 Sarem
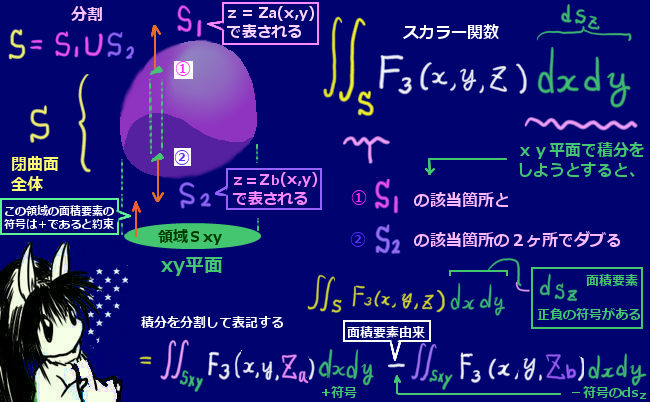



証明 ガウスの発散定理 理数系無料オンライン学習 Kori



グリーンの定理 積分定理の王
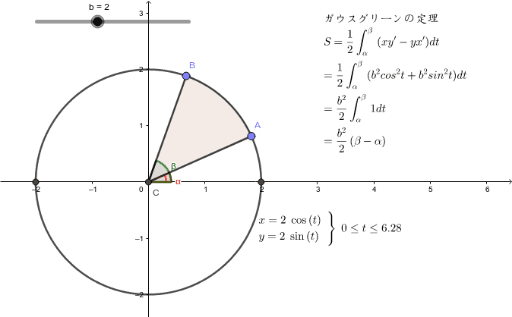



ガウスグリーンの定理 Geogebra



ガウスの発散定理 ベクトル解析 基礎からの数学入門




補足の補足 電磁気学 28 静電シールド 27 数学 ガウスの定理 その1 Jo3krpの独り言




ガウス グリーンの定理 例題 Youtube



グリーンの定理 積分定理の王




グリーンの定理の証明



ガウスの発散定理 物理のかぎしっぽ



Ibe Kagoshima U Ac Jp



Wakayama U Ac Jp




アルパカ 極座標の面積公式の証明 理系 落ちこぼれkの東大受験日記



グリーンの定理 積分定理の王




講師 幹 浩文 A314 微分 ベクトル解析 15 まとめ 講師 幹 浩文 A314 A103 10 50 12 金 Ppt Download



グリーンの定理 積分定理の王 赤赤 新浪博客



ねこ騙し数学
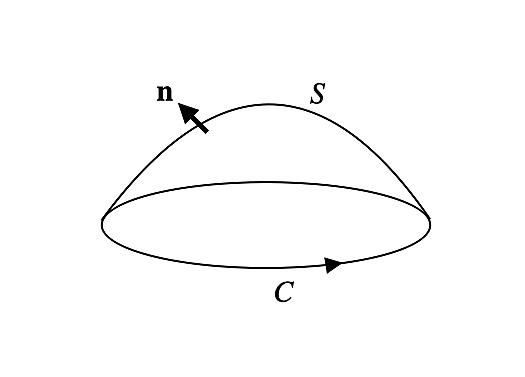



ストークスの定理とは サイエンスの人気 最新記事を集めました はてな



第13回 グリーン ガウス ストークスの定理



グリーンの定理の例による理解と証明 応用 趣味の大学数学



14章 ベクトルの発散とガウスの発散定理とグリーンの定理
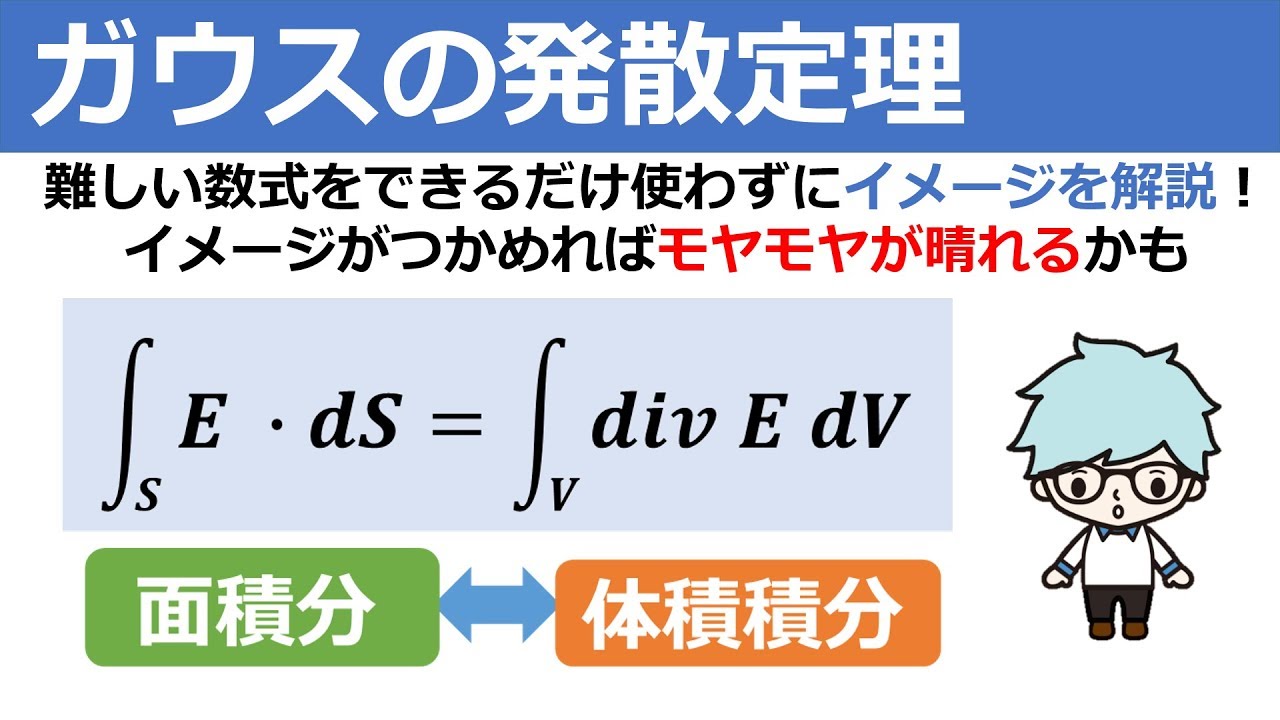



ガウスの発散定理をイメージで理解 Youtube




カマキリ Python頑張る昆虫 どこが ガウスの発散定理 かわからないけど これは グリーンの定理 のことかな



グリーンの定理 積分定理の王




ガウスの発散定理 2次元 の証明と式の意味 数学 ベクトル解析 Gauss Theorem Youtube



グリーンの定理 積分定理の王



3 13 ガウスの定理




大学 講義 ベクトル解析 05 L09 体積分 球座標 ベクトル場の発散div Vと3次元のガウスの発散定理 Youtube




書記が数学やるだけ 135 ストークスの定理 ガウスの発散定理 連続の式 ヘルムホルツ分解 Malinka書記 Note




直角双曲線の面積公式 Den Of Hardworking



グリーンの定理 積分定理の王
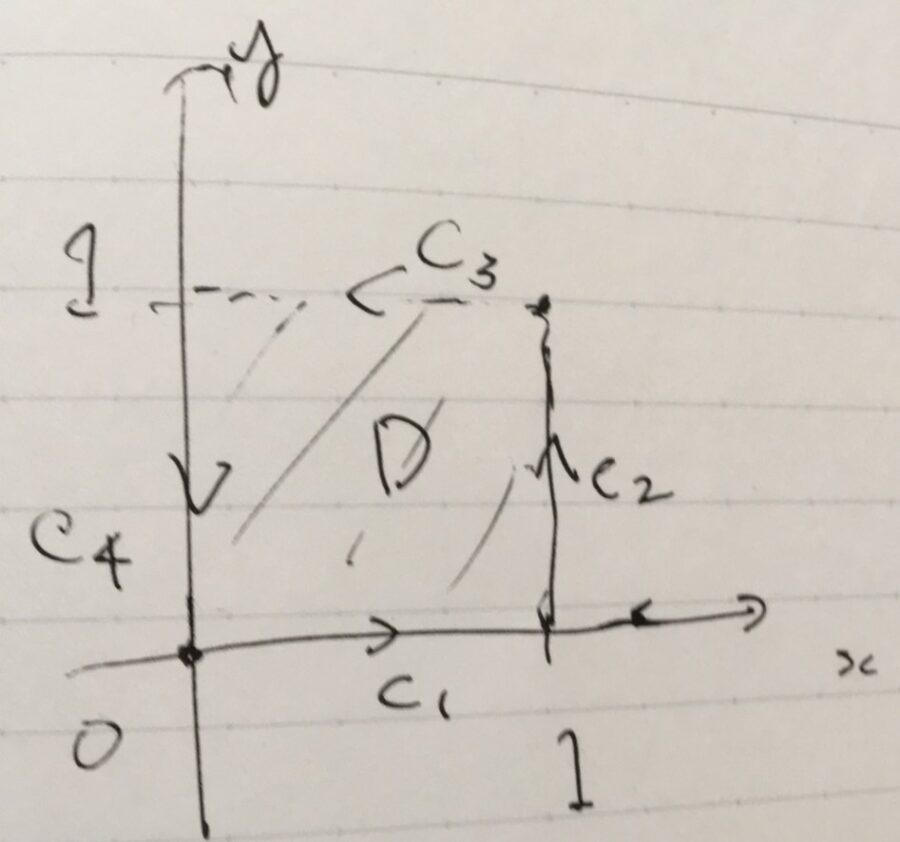



グリーンの定理の例による理解と証明 応用 趣味の大学数学



Ibe Kagoshima U Ac Jp




第13回 グリーン ガウス ストークスの定理



板橋村だより 数学セミナー 29 ガウスの定理 ストークスの定理



ガウスの法則 ガウスの法則の微分形 ガウスの定理 電磁気学入門



電磁気学で使うベクトル解析入門 グリーンの定理 ストークスの定理 Gradの勾配
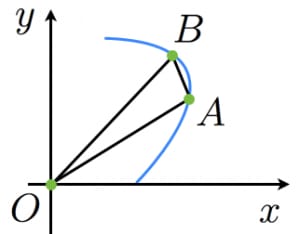



ガウスグリーンの定理の入試への応用 高校数学の美しい物語




Y Tx 型のパラメーター曲線にはガウス グリーンの定理 Den Of Hardworking



ガウスの発散定理 物理のかぎしっぽ




いぷの数学ツイをrtするbot 手動 Epsilon Rt Bot Twitter
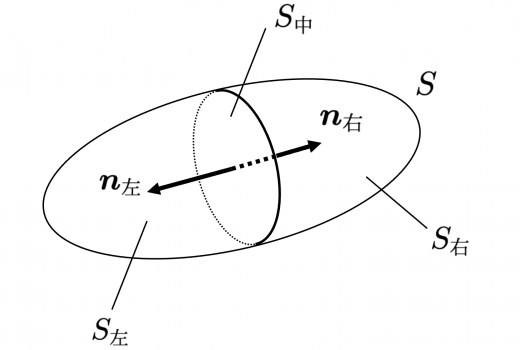



ガウスの発散定理 ストークスの定理の証明 高校数学の美しい物語



グリーンの定理 積分定理の王



0 件のコメント:
コメントを投稿